GUIA DE ESTUDIO No. 1
Semana del 16 al 20 de marzo
Prof: Félix Antonio García Aroche
Materia: Matemática I
Grado: Primero Básico
Secciones: E y F
Tema: Unión de
conjuntos
En
la teoría de conjuntos, la unión de
dos (o más) conjuntos es una operación que resulta en otro conjunto,
cuyos elementos son los mismos de los
conjuntos iniciales. Por ejemplo, el conjunto de los números naturales es la unión del conjunto
de los números pares positivos P y el
conjunto de los números impares positivos I:
Ejemplos
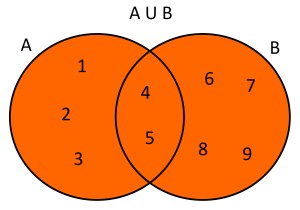
Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la unión de estos conjuntos será A∪B={1,2,3,4,5,6,7,8,9}. Usando diagramas de Venn se tendría lo siguiente:
EJERCICIO No. 1
Resuelva los siguientes
ejercicios de Unión de conjuntos en
forma enumerativa y en forma gráfica. Resolverlos en hojas tamaño cuadrícula
tamaño carta y archívelas en un folder que se revisará de regreso a clases.
1) A=
( 1, 2,4,6,8) B=
(1,3,5,7,8)
2) A=
( a, e ,i, o, u) B= ( a,
b, c, d, e, f)
3) A= ( l, u, n, e, s) B= (l, u, n, a)
4) A= (j, u, l, i ,a, n) B= (j, u, l, i, o)
5) A= ( 2,3,4,8,9) B= (3,6,9,12,15)
link de consulta:
https://www.ejemplos.co/20-ejemplos-de-union-de-conjuntos/
cualquier duda pueden escribir al correo: profe.felixgarciainma@gmail.com
__________________________________________________________________________________________________________________________________________________________________
GUIA DE ESTUDIO No. 2
Semana del 23 al 27 de marzo
Prof: Félix Antonio García Aroche
Materia: Matemática I
Grado: Primero Básico
Secciones: E y F
INSTRUCCIONES: Copiar en el cuaderno la siguiente teoría.
INTERSECCIÓN DE CONJUNTOS
·
La intersección de
dos (o más) conjuntos es
una operación que resulta en otro conjunto que
contiene los elementos comunes o (repetidos) a los conjuntos de partida o iniciales.
Ejemplo:
Sean los conjuntos
A= ( 1,2,3,4,5)
B= (4,5,6,7,8,9)
AnB = ( 4,5)
Ejercicio 2:
Resuelva la operación de intersección en hojas adicionales y archiveles en el folder, los siguientes conjuntos en forma enumerativa y en forma gráfica.
A= ( 2,4,6,8) B= ( 1,2,3,4,5)
|
A= ( a, b, c,
d, e, f, g) B= ( a ,e ,i, o, u)
|
A= (1,2,3,4,5,6,7)
B= (1,3,5,7,9)
|
A= ( m ,a ,n,
,z) B= (b, a, n, o)
|
A= ( 1,3,6,9) B= (1,2,3,4,6)
|
A= (a, c, e, z, m, y) B= ( s, m, t, v, y)
|
cualquier duda pueden escribir al correo: profe.felixgarciainma@gmail.com
__________________________________________________________________________________________________________________________________________________________________
GUIA DE ESTUDIO No. 3
Semana del 30 DE MARZO AL 3 DE ABRIL
Prof: Félix Antonio García Aroche
Materia: Matemática I
Grado: Primero Básico
Secciones: E y F
EJERCICIO 3. UNIÓN DE CONJUNTOS
Instrucciones: Copiar en hojas los ejercicios de la pag. 24 y pag 25 y resolverlos en forma enumerativa y en forma gráfica utilizando diagramas de Venn. las hojas deberá archivarlas en un folder. y completar en el libro únicamente en forma enumerativa.
EJERCICIO 3. UNIÓN DE CONJUNTOS
Instrucciones: Copiar en hojas los ejercicios de la pag. 24 y pag 25 y resolverlos en forma enumerativa y en forma gráfica utilizando diagramas de Venn. las hojas deberá archivarlas en un folder. y completar en el libro únicamente en forma enumerativa.
cualquier duda pueden escribir al correo: profe.felixgarciainma@gmail.com
_________________________________________________________________________________________________________________________________________________________________
SEMANA SANTA
Semana del 6 AL 10 DE ABRIL
Prof: Félix Antonio García Aroche
Materia: Matemática I
Grado: Primero Básico
Secciones: E y F
REPASAR LOS CONTENIDOS VISTOS.... !!!!!!QUÈDATE EN CASA!!!!!!
__________________________________________________________________________________________________________________________________________________________________
REPASAR LOS CONTENIDOS VISTOS.... !!!!!!QUÈDATE EN CASA!!!!!!
__________________________________________________________________________________________________________________________________________________________________
GUIA DE ESTUDIO No. 4
Semana del 13 AL 17 DE ABRIL
Prof: Félix Antonio García Aroche
Materia: Matemática I
Grado: Primero Básico
Secciones: E y F
EJERCICIO 4. INTERSECCIÓN
DE CONJUNTOS
Instrucciones: Copiar en hojas los ejercicios de la pag. 28 y pag 29 y resolverlos en forma enumerativa y en forma gráfica utilizando diagramas de Venn. las hojas deberá archivarlas en un folder. y completar en el libro únicamente en forma enumerativa.
___________________________________________________________________________________________________________
GUIA DE ESTUDIO No. 5
Semana del 20 AL 24 DE ABRIL
Prof: Félix Antonio García Aroche
Materia: Matemática I
Grado: Primero Básico
Secciones: E y F
Instrucciones: Copiar la siguiente informaciòn en hojas y resolver el ejercicio en hojas tamaño carta y archivarlas en un folder... o bien trabajar en el libro la pag. 32
LA DIFERENCIA
ENTRE CONJUNTOS
Es un nuevo conjunto formado por elementos que pertenecen al
primer conjunto y que no pertenecen al segundo conjunto. El símbolo es - un signo menos.
Por ejemplo Sean los conjuntos
A=(
a,b,c,d,e)
B= (
c,d,e,f,g)
A -
B = ( a,b)
Aquì podemos
notar que al quitarle los elementos que son iguales entre ambos conjuntos, se
escriben únicamente los que quedan o los restantes del primer conjunto osea A.
cualquier duda pueden escribir al correo: profe.felixgarciainma@gmail.com
____________________________________________________________________________________________________________
GUIA
DE ESTUDIO No. 6
Semana del 8 al 12 de junio
Prof: Fèlix Garcia
Materia: Matemática I
Grado: Primero Básico
Secciones: E,F
INSTRUCCIONES: copiar la siguiente información en hojas y archive en un folder
DIFERENCIA SIMÉTRICA ( )
La operación Diferencia
simétrica entre conjuntos es un nuevo conjunto formado por la UNION de las DOS
diferencias simples de los conjuntos que nos dan. El símbolo de la diferencia
simétrica es “∆”
EJEMPLO: Sean los
conjuntos A= { a,b,c,d } B= { b,c,d,e,f }
A ∆ B = ( A-B) U ( B-A)
Primero:
se realizan las diferencias simples
( A – B
) & ( B – A )
Obteniendo los siguientes conjuntos
A – B = { a }
B – A = { e, f }
Segundo:
se realiza la unión de las diferencias simples
A ∆ B = (A-B) U (B-A)
A ∆ B = {a}
U {e,f }
A ∆ B = { a, e, f }
TAREA: resolver en hojas o en el libro los ejercicios indicados. Páginas 33,34 y3
__________________________________________________________________________________________________________
GUIA DE ESTUDIO No. 7
Semana del 22 al 26 de Julio
Prof: Félix Antonio García Aroche
Materia: Matemática I
Grado: Primero Básico
Secciones: E y F
COPIE LA SIGUIENTE INFORMACIÒN EN HOJA Y ARCHIVAR EN UN FOLER
LOS NÚMEROS NATURALES.
El número en
la actualidad es la idea de cantidad. El
numeral, es el símbolo que se utiliza, según la cultura de que se trate, para
representar la idea de la cantidad.
Cuando se trabaja con símbolos, decimos el número 10, y debería decirse
el numeral 10. Pero ya es una costumbre
muy antigua que no se puede quitar
LOS NUMEROS
NATURALES:
De los
conjuntos numéricos bien sistematizados y organizados, se cree que el de los números
naturales fue el primero en la historia de la humanidad.
Se cree que
el primer conjunto que nació es el de los números dígitos (0,1,2,3,4,5,6,7,8,9)
llamados así por ser un conjunto coordinable con los dedos de las manos. Luego el valor posicional nació en gran conjunto
de números naturales. ( 0.1.2.3.4.5.6.7.8.9.10.11.12.13.14.15…etc)
OPERACIONES QUE SE PUEDEN REALIZAR
CON NUMEROS NATURALES
IGUALDAD
O ECUACIONES:
Ejemplo:
10 + X = 28
10+ 18 = 20 solución X= 18
20 + x = 30
20 + 10 = 30 solución 10
15 + X = 21
15+6 = 21 solución 6
RESTA.
15 -3 = 12
50 – 50 = 0
14 – 3 = 11
MULTIPLICACIÒN DE NATURALES:
Qué valor debe tener X par que: X * 5 =
15
X
= 3
Porque 3 x 5 = 15
qué valor debe tener X, para que:
X * 8 = 40
X =
5
Porque 5 X 8 = 40
Escribir como suma los siguientes multiplicandos:
3X 5 = 5 + 5 + 5 = 15
5 X 4 = 4+4+4+4+4= 20
DIVISIÒN DE LOS NATURAELS:
48 / 8 = 6
24/ 24 = 1
9/ 3 = 3
Realizar una pequeña investigación, escrita en el cuaderno de las
propiedades de la división
TAREA: Resolver En el
libro las pag. De 46 a 51
v En las siguientes paginas están
las imágenes de las hojas del libro.
cualquier duda pueden escribir al correo: profe.felixgarciainma@gmail.com
o al what app. 3133-3335
____________________________________________________________________________________________________________
GUIA DE ESTUDIO No. 8
Semana del 13 al 17 de Julio
Materia: Matemática I
Grado: Primero Básico
Secciones: E y F
COPIE LA SIGUIENTE INFORMACIÒN EN HOJAS Y ARCHIVAR EN UN FOLDER
POTENCIACIÒN CON NATURALES:
Ejemplo:
a) 93 = 9X9x9 = 729
b) 72 = 7X 7 = 49
PROPIEDADES
DE LA POTENCIACIÒN
·
Multiplicaciòn
de Potencia de Igual Base:
a m X a n = a (m+n)
Ejemplo: 5 2 X 5 4 =
5 ( 2+4) = 7 = 78125
32 X 3 3
=
3 ( 2 + 3 ) = 5 = 243
·
Potencia de otra potencia
(a m ) n
= a (m x n )
Ejemplo: ( 23 )4 = 2
(3x4) = 12 = 4096
( 4 2
) 5 = (4
) (2x5) = 10
= 1048576
·
Potencia
de un producto
( a x b) m = am X
b m
Ejemplo: ( 3 x 4 )2 = 32 X 42
= 9 X 16 = 144
·
Divisiòn de potencia de igual base.
am / a n = a m – n
5 6 / 54
= 5
(6 – 4 ) = 2 = 25
RADICACIÒN EN LOS
NATURALES..
Radical es una expresión en forma n √ a
Ejemplo_ √
25 =
5
√64 = 8
PROPIEDADES DE LA RADICACIÒN
·
Potencia de una Raìz
6 √ 5 18 = 5
18/6 = 3 = 5 3 = 125
·
Raìz
de un Producto
3√ 64 x
343 = 3√64 X
3√ 343
= 4 X
7 = 28
·
Raìz
de un diviòn
3 √ 64
/ 3 √ 8 = 4 /
2 = 2
·
Raìz
de otra raíz
3 √ 2 √ 15625 = 3x2
= 5√ 15625 = 5
EJERCICIO:
TAREA:
Resolver en
el libro las siguientes páginas.
de la 55 a
59.
cualquier duda pueden escribir al correo: profe.felixgarciainma@gmail.com
o al what app. 3133-3335
____________________________________________________________________________________________________________
GUIA DE ESTUDIO No. 9
Semana del 20 al 24 de Julio
Prof: Félix Antonio García Aroche
Materia: Matemática I
Grado: Primero Básico
Secciones: E y F
DIVISIBILIDAD
INSTRUCCIONES:
COPIE LA SIGUIENTE INFORMACIÒN EN
HOJAS Y ARCHIVAR EN FOLDER
Divisibilidad
Numero
Primo: es el número que solamente es divisible por la unidad y por el mismo
Numero
compuesto: Definiciòn un número “a” es compuesto si a= b X C para todo b y c diferente de +1 y -1.
Multiplo:
Mùltiplo de otro número b, es otro número a talque a = b
Ejemplos:
Hallar el mcm
18 2
9 3 = 2x3x3 = 18
3 3
1
NOTACIÒN
CIENTÌFICA:
Es una forma
abreviada de escribir un número tomando como base 10
Ejemplo
3,465
3X1000 =
3000
4X100 = 400
6X10 = 60
5x 1 = 5
Equivale a
: 3 .465 x 103
54862
5 X 10000 =
50000
4X 1000 = 40000
8X100 = 800
6x10 = 60
2x 1 = 2
EQUIVALE 5. 4862 X 104
SISTEMA DE
NUMERACIÒN MAYA
Este sistema
utiliza de base el numero 20 y su valores son posicionales
160000
|
8000
|
400
|
20
|
1
|
= 1
=5
= 0
Ejemplo
|
1 X 400 =
|
400
|
|||
 |
5 x 20 =
|
20
|
|||
  |
1X1 =
|
1
|
421
EL SIGUIENTE
TRABAJO VA SOLO EN EL LIBRO…..SINO TIENE LIBRO PUEDE HACERLO EN HOJAS.
TAREA: RESPONDER LAS PAG.
56,57,58,59,60,61,63,68,69
cualquier duda pueden escribir al correo: profe.felixgarciainma@gmail.com
o al what app. 3133-3335
____________________-------_________________________-
GUIA DE ESTUDIO No. 10
Semana del 27 al 31 de Julio
Prof: Félix Antonio García Aroche
Materia: Matemática I
Grado: Primero Básico
Secciones: E y F
INSTRUCCIONES:
COPIE LA SIGUIENTE INFORMACIÒN EN
HOJAS Y ARCHIVAR EN FOLDER
CONJUNTO
DE ENTEROS.
Se le llama
enteros a al conjunto de numero
positivos y negativos… que se pueden representar en una recta numérica.
Valor
Absoluto:
Es el valor real de un número sin importar su signo. El símbolo son dos líneas paralelas.
Ejemplo:
+8 = 8 |
|
||
-6
= 6
PLANO
CARTESIANO,
Es un intersección
de punto de acuerdo a una pareja ordena ( x,Y)
COMPARACIÒN
DE NUMEROS ENTEROS
= IGUAL
‹
MENOR QUE
›
MAYOR QUE
Ejemplos:
-2 ‹ 6
7 ›
-1
Conclusión: Un número entre más a la derecha
este en la recta numérica tiene mayor valor absoluto.
OPERACIONES.
Suma:
(+8) + (+15) = +23
(-4 ) + (-6
) = -10
Resta:
(34 ) – (10)
= 24
(25) – (-25)
= + 50
(18 ) – (+3)
= 15
Multiplicaciòn
(5) x( 4) = 20
(-3 ) x (-6)
= + 18 (ley de signos)
(-7 ) x ( +
5) = - 35 (ley de signos)
Divisòn
10 / 2
= 5
-8 / -2
= +4
30 / -5 = -6
-24/ 3 = -8
FIN DE LAS
GUIAS…
TRABAJO SOLO EN EL LIBRO:
Resolver las pag.
73 a 85
cualquier duda pueden escribir al correo: profe.felixgarciainma@gmail.com
o al what app. 3133-3335
___________________________________________.
_____________________________________________________________________
___________________________________________.
_____________________________________________________________________
Como se efectua el ejercicio de la pag 32 de la diferencia simple ejemplo M-M como va colocado graficamente disculpe es que no entiendo
ResponderEliminar